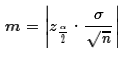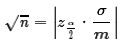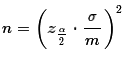Find Sample Size for specified Margin of Error
Return to Topics page
We start with a quick review.
The process of computing a confidence interval
in the case where we know the
population standard deviation and where
we have a sample of size n that yields a
sample mean  is
as follows:
is
as follows:
- From the confidence level compute the
value of
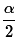 using
using
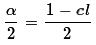
- Use qnorm(
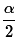 )
to find the associated z-score,
)
to find the associated z-score,
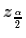
- Find the margin of error as
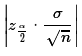
- Find the two parts to the confidence interval by evaluating
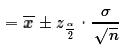
We notice that the margin of error is calculated from three things:
the confidence level we choose, the standard deviation
of the population, and the sample size.
If we know the first two, we can choose the last one, the sample size,
to produce a margin of error that is as small as we want.
Consider the case where we know that the population standard deviation
is 18.23 and where we know that we want a 95% confidence
interval. Our margin of error will be the value
of the expression 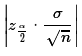 .
However, in that expression we know that σ=18.23
and we determine that
.
However, in that expression we know that σ=18.23
and we determine that 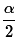 =0.025,
which means that we can use qnorm(0.025) to find
=0.025,
which means that we can use qnorm(0.025) to find
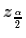 = -1.96.
The absolute value in the expression for the margin of error
means that our margin of error now simplifies to
1.96*18.23/sqrt(n) = 35.7308/sqrt(n).
If we choose n to be 16 then sqrt(16)=4 and our
margin of error becomes 35.7308/4, a number just smaller
than 9.
What if we want the margin of error to be less than 7?
Then we need to have the denominator be a little bit larger than 5.
To do that we need the sample size to be a little bigger than 25.
How much bigger? We could try 26. Then sqrt(26)≈5.099and
35.7308/5.099≈7.007. Close, but not less than 7.
Try sample size=27.
Then sqrt(27)≈5.196and
35.7308/5.196≈6.876, well below our goal of 7.
Therefore, before we even start to take a random sample of the population,
we know that if we take a sample of size 27 then our margin of error
will be 6.876.
= -1.96.
The absolute value in the expression for the margin of error
means that our margin of error now simplifies to
1.96*18.23/sqrt(n) = 35.7308/sqrt(n).
If we choose n to be 16 then sqrt(16)=4 and our
margin of error becomes 35.7308/4, a number just smaller
than 9.
What if we want the margin of error to be less than 7?
Then we need to have the denominator be a little bit larger than 5.
To do that we need the sample size to be a little bigger than 25.
How much bigger? We could try 26. Then sqrt(26)≈5.099and
35.7308/5.099≈7.007. Close, but not less than 7.
Try sample size=27.
Then sqrt(27)≈5.196and
35.7308/5.196≈6.876, well below our goal of 7.
Therefore, before we even start to take a random sample of the population,
we know that if we take a sample of size 27 then our margin of error
will be 6.876.
What if we want the margin of error to be even smaller, say less than
or equal to 2?
We need 35.7308/sqrt(n) to be less than 2.
Clearly, a denominator of 18 will work, and that
would mean that we would want sample size of 18*18=324.
But could we use 323? The sqrt(323) is about 17.9722
and 35.7308/17.9722≈1.988, so 323 would work,
but what about 322?
This "guessing and checking" is not a good approach.
We should be able to do much better! The original formula for
the margin of error, m was
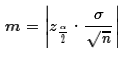 This is equivalent to
This is equivalent to
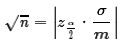 But then we could square both sides to get
But then we could square both sides to get
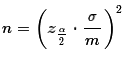 For the problem above, using a 95% confidence level and a
population that has a standard deviation of
18.23, find the smallest sample size that
will produce a margin of error that is 2 or less,
we could evaluate the right-hand side of that expression in R
as shown in Figure 1.
For the problem above, using a 95% confidence level and a
population that has a standard deviation of
18.23, find the smallest sample size that
will produce a margin of error that is 2 or less,
we could evaluate the right-hand side of that expression in R
as shown in Figure 1.
Figure 1

We cannot have a sample size of 319.1608, and we know that
increasing the sample size decreases the margin of error.
Therefore, we always round the answer up to the next highest whole number,
in this case 320.
Were we looking for the smallest sample size that is required
to have the margin of error be 3 or less then we use the
command in Figure 2.
Figure 2

Our answer would be to use 142 as the sample size.
Or, if we want the smallest sample size that generates a
confidence interval with the margin of error being
4.25 then the computation would be as in Figure 3.
Figure 3

Our answer would be to use 71 as the sample size.
The formula is not difficult to evaluate, but it is a pain to remember.
We could just create a function to do this for us.
A "quick and dirty" function, one without any of the
checks on the appropriateness of the values sent to it,
would be
find_samp_size <- function( sigma, cl, moe)
{
z <- qnorm( (1-cl)/2)
quotient <- ( z * sigma / moe)^2
if (as.integer( quotient) != quotient )
{ quotient <- as.integer(quotient) + 1}
return( quotient )
}
Figure 4 shows that function and three applications of it
to do the three problems that we did in Figures 1 through 3.
Figure 4

Worksheet for Finding Sample Size
Here is a link to a worksheet
with randomly generated problems related to
finding the required sample size for a given confidence level and a
known population standard deviation.
Return to Topics page
©Roger M. Palay
Saline, MI 48176 December, 2015
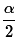 using
using
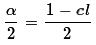
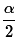 )
to find the associated z-score,
)
to find the associated z-score,
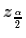
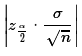
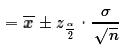
 is
as follows:
is
as follows:
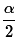 using
using
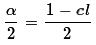
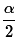 )
to find the associated z-score,
)
to find the associated z-score,
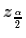
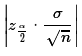
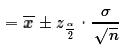
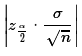 .
However, in that expression we know that σ=18.23
and we determine that
.
However, in that expression we know that σ=18.23
and we determine that 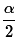 =0.025,
which means that we can use qnorm(0.025) to find
=0.025,
which means that we can use qnorm(0.025) to find
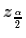 = -1.96.
The absolute value in the expression for the margin of error
means that our margin of error now simplifies to
1.96*18.23/sqrt(n) = 35.7308/sqrt(n).
If we choose n to be 16 then sqrt(16)=4 and our
margin of error becomes 35.7308/4, a number just smaller
than 9.
What if we want the margin of error to be less than 7?
Then we need to have the denominator be a little bit larger than 5.
To do that we need the sample size to be a little bigger than 25.
How much bigger? We could try 26. Then sqrt(26)≈5.099and
35.7308/5.099≈7.007. Close, but not less than 7.
Try sample size=27.
Then sqrt(27)≈5.196and
35.7308/5.196≈6.876, well below our goal of 7.
Therefore, before we even start to take a random sample of the population,
we know that if we take a sample of size 27 then our margin of error
will be 6.876.
= -1.96.
The absolute value in the expression for the margin of error
means that our margin of error now simplifies to
1.96*18.23/sqrt(n) = 35.7308/sqrt(n).
If we choose n to be 16 then sqrt(16)=4 and our
margin of error becomes 35.7308/4, a number just smaller
than 9.
What if we want the margin of error to be less than 7?
Then we need to have the denominator be a little bit larger than 5.
To do that we need the sample size to be a little bigger than 25.
How much bigger? We could try 26. Then sqrt(26)≈5.099and
35.7308/5.099≈7.007. Close, but not less than 7.
Try sample size=27.
Then sqrt(27)≈5.196and
35.7308/5.196≈6.876, well below our goal of 7.
Therefore, before we even start to take a random sample of the population,
we know that if we take a sample of size 27 then our margin of error
will be 6.876.