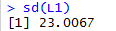Descriptive Statistics: Population vs. Sample

Return to Topics page
In the arrangement of web pages for this course, this page presents no new material. It is provided here because after we start seriously talking about samples versus populations, it make sense to review how we name and apply certain descriptive measures.

We distinguish between population and sample characteristics by referring to population characteristics as population parameters and sample characteristics as sample statistics. Thus, the mean of a population is a parameter of that population, but the mean of a sample is a statistic of that sample. Beyond that distinction there is no difference in the naming or computing for the measures mode, the median, the range, and the quartiles. The mean of a population, μ, has a different symbol from the one used for the mean of a sample, , however the computation of each is the same. Standard deviation has both different symbols, σ for a population and s_x for a sample, and slightly a slightly different formula. These differences are presented in the following table.

As an example, we start with the data in Table 2:
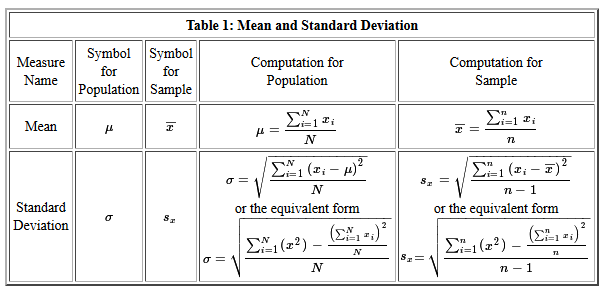
Figure 1 holds the console image of running the commands:

gnrnd4( key1=740587104, key2=0002300357 )
L1
mean(L1)
summary(L1)

Figure 1

The values in Table 1, and now in L1 in our R session, could be a population or they could be a sample. In either case, the command mean(L1) displays the value of the mean of those values. If Table 1 represents a population then we would say μ = 356.375 but if those value represent a sample then we would say = 356.375.

Figure 1 continues with the summary(L1)command. The result also displays the mean but with fewer significant digits. Of course, the other values in that display have the same meaning independent of the values being a population or a sample.

To find the standard deviation of the values in Table 1 we use the sd(L1) command as shown in Figure 2.

Figure 2

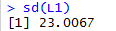
The result, 23.0067, assumes that the values in Table 1 are from a sample. There is no way to tell the sd() command that you want the values to be considered a population.

If we do want the standard deviation for a population we can just multiply the sd() result by sqrt((N-1)/N) where N is the number of values in the table. Table 1 has 72 values in it so we use the command sd(L1)*sqrt(71/72) to compute the standard deviation of the values assuming they are from a population. The result is shown in Figure 3

Figure 3

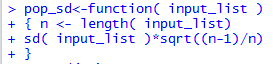
You may recall that in our earlier page discussing this issue we developed a function to do our work for us. The code of that function was

pop_sd<-function( input_list )
{ n <- length( input_list)
sd( input_list )*sqrt((n-1)/n)
}

Figure 4 shows the definition of the function in our R session.

Figure 4

Once the function is defined we can use it to compute the population standard deviation by just calling the function as in pop_sd(L1). Figure 5 shows the use of that command.

Figure 5