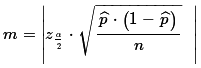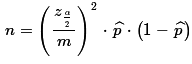Confidence Interval for a Population Proportion
Return to Topics page
In the case where
we have a population where some of the elements in that
population have a specific characteristic,
we talk about the proportion of the population that has
that characteristic. We generally signify that
proportion as p.
If we take a sample of size n of that population
and in that sample we find x items with the
characteristic, then the value
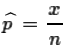 is a
point estimate for p. We want a confidence interval
for p derived from the sample.
That confidence interval will be
point estimate ± (margin of error)
is a
point estimate for p. We want a confidence interval
for p derived from the sample.
That confidence interval will be
point estimate ± (margin of error)
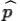 ± (margin of error)
The we recall that for cases where n*p≥10 and
n*(1-p)≥10 we have the distribution of
± (margin of error)
The we recall that for cases where n*p≥10 and
n*(1-p)≥10 we have the distribution of
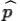 is
normal with mean = p and
standard deviation = √p*(1-p)/n.
Therefore, for a specified confidence level we can
find zα/2 to make the
margin of error =
is
normal with mean = p and
standard deviation = √p*(1-p)/n.
Therefore, for a specified confidence level we can
find zα/2 to make the
margin of error =  That makes the confidence interval be
That makes the confidence interval be
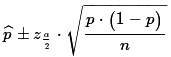 Of course, the problem with this is that we do not know
the value of p so we cannot compute that formula.
Of course, the problem with this is that we do not know
the value of p so we cannot compute that formula.
Instead, if we change our special conditions, we
can use 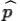 instead of p
in the approximation of the standard deviation.
The new restrictions are
instead of p
in the approximation of the standard deviation.
The new restrictions are
- The sample size n is no more than 5% of the population size.
(Another, popular, way to say this is that the population size is
more than 20 times the sample size, n.)
- Population items either have the characteristic or the do not.
That is another way of saying that the population items fall into
one of two categories, those with the characteristic and those
without the characteristic.
- The sample must contain at least 10 items in each of the two categories.
If these conditions are met then we can use
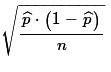 as
the approximation of the standard deviation of the
as
the approximation of the standard deviation of the
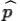 's.
That gives the formula
's.
That gives the formula
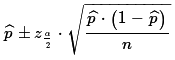 to use to find the desired confidence interval
for the population proportion p based on a
sample of size n with x items in the
sample having the characteristic so that
to use to find the desired confidence interval
for the population proportion p based on a
sample of size n with x items in the
sample having the characteristic so that
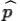 =x/n.
=x/n.
An example is in order here.
We start with a population of enormous size,
something having over 20,000
items. We take a sample of size 73 (this is less than 5%
of the population so we are OK on that point).
Of the 73 items, 17 have a certain characteristic.
That means that 73-17=56 items do not have the characteristic.
(There are more than 10 items that do and 10 items that do not
have the characteristic in the sample.
,
so we are OK on that point).
Then we can compute an approximation to the sample proportion
as 17/73 ≈0.233, which means that
(1-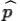 ) ≈ 0.767.
We use those values to compute an approximation to the
standard deviation of sample proportions as
√p*(1-p)/n = √0.233*0.767/73 ≈ 0.049.
) ≈ 0.767.
We use those values to compute an approximation to the
standard deviation of sample proportions as
√p*(1-p)/n = √0.233*0.767/73 ≈ 0.049.
To find the 95% confidence interval from 17 items out of
73 in the sample,
we need to find the
zα/2 that gives
us 95% of the area under the curve between
zα/2 and
-zα/2.
We can use the table,
a calculator, or the qnorm(.025) statement to do this.
That value turns out to be 1.96.
With all that the confidence interval
becomes 0.233 ± 1.96*0.0.049 ≈ 0.233 ±0.096
or (0.137,0.329).
All that computation is captured in the R
statements:
x <- 17
n <- 73
p_hat <- x/n
p_hat
p_hat_sd <- sqrt(p_hat*(1-p_hat)/n)
p_hat_sd
alpha_div_2 <- (1-0.95)/2
alpha_div_2
z <- abs( qnorm( alpha_div_2))
z
lower <- p_hat - z*p_hat_sd
upper <- p_hat + z*p_hat_sd
lower
upper
Figure 1 shows the console view of performing those statements.
Figure 1
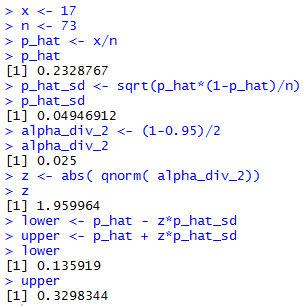
The difference between our earlier hand computed
confidence interval and the one shown in Figure 1
is that the former involved some significant rounding in
the approximations that we made. The latter still has approximations,
but the values are carried for many more digits.
We could do many more examples, but they all follow the same computations
shown in Figure 1.
As we have done before, we can codify those computations in
a function. All we need to do is to feed the
function the values of n, p, and the
desired confidence interval. Then we
let the function perform all of the required computations.
One such function is defined by:
ci_prop <- function( n, x, cl=0.95)
{
# compute a confidence interval for the
# proportion given the sample size, the
# number of items with the characteristic,
# and the confidence level
# do a few checks on the information given
if( cl <=0.0 | cl >= 1 )
{return("Confidence level needs to be between 0 and 1")}
if( x < 10)
{return("Need at least 10 items with the characteristic")}
if( n-x < 10)
{return("Need at lease 10 items without the characteristic")}
# we have no way to check if we are sampling < 5%
# of the population
p_hat <- x/n
p_hat_sd <- sqrt(p_hat*(1-p_hat)/n)
alpha_div_2 <- (1-cl)/2
z <- abs( qnorm( alpha_div_2))
lower <- p_hat - z*p_hat_sd
upper <- p_hat + z*p_hat_sd
if(lower < 0) { lower<-0}
if(upper > 1 ) { upper <- 1}
result<-c(lower, upper, p_hat, z, p_hat_sd)
names(result) <- c("lower", "upper", "p hat",
"z-score", "p hat sd")
return( result )
}
Once defined we can use the statement ci_prop(73, 17, .95)
to do all of the work that we saw back in Figure 1. This
is shown in Figure 2.
Figure 2

Now that we have the ci_prop() function available
it is easy to try out some other situations.
Look at what we can learn from doing:
ci_prop(73,10,.95)
ci_prop(73,7,0.95)
ci_prop(73,64,0.95)
ci_prop(73,17,0.90)
ci_prop(73,17,0.80)
ci_prop(73,17,0.99)
The console report on these is given in Figure 3.
Figure 3

The results shown in Figure 3 illustrate
the effect of having a smaller  ,
of having too small a value for x, of having a too large
value for x, and of changing the desired confidence level.
Of particular note is the fact that by lowering the
desired confidence level we make the
confidence interval smaller.
,
of having too small a value for x, of having a too large
value for x, and of changing the desired confidence level.
Of particular note is the fact that by lowering the
desired confidence level we make the
confidence interval smaller.
Let us look at making the confidence interval
narrower by increasing the sample size. In our original
example we found 17 of 73 items have the identified characteristic.
If we had a sample of 146 and found 34 with the
desired characteristic, then our  would not have changed. However, with the larger sample
size we will get a narrower confidence interval.
Figure 4 show a few examples where the
sample proportion does not change but the sample size does.
would not have changed. However, with the larger sample
size we will get a narrower confidence interval.
Figure 4 show a few examples where the
sample proportion does not change but the sample size does.
Figure 4
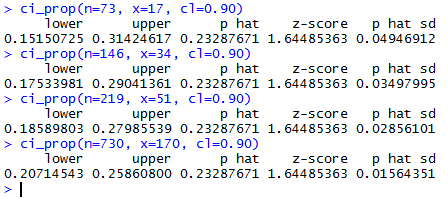
We can make the margin of error,
half the width of the confidence interval, as small as we
want by increasing the sample size. To some extent this is true.
Remember that we start with the
margin of error =  and then realized that we had to use the approximation
involving
and then realized that we had to use the approximation
involving 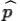 , namely,
, namely,
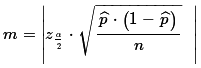 We could solve that equation for n to get
We could solve that equation for n to get
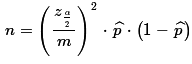 This seems to give us a way to determine the required
sample size, n, if we have the other values,
including a desired margin of error.
This seems to give us a way to determine the required
sample size, n, if we have the other values,
including a desired margin of error.
The problem with this is that we cannot be
sure that we will get the same proportion
of items with the specified characteristic in
a new sample. If we use the situations illustrated
in Figure 4 we see that the proportion
is about 0.23287671, really 17/73.
If we want a margin of error = 0.02,
then the formula we just found tells us that
n = (1.64485363/0.02)²*(17/73)(56/73)
or about 1208.33.
Even if we round that off to 1241, the first
whole number larger than 1208 that is evenly divisible by 73,
there is no reason why, if we took a sample of
1241 items that we would have the same 17/73 of
them, 289 of them, having the specified characteristic.
Most likely we will be close, but we just cannot be sure.
One final note here is that although we stated above that the
population was enormous, we also qualified that by saying
that it had over 20,000 items.
If we wanted to take a sample of size 1241
we need to be sure that we are not sampling more than 5%
of the population. But 5% of 20,000 is 1,000. We need to
be sure that the population has more than 20 times the 1241,
that is, 24,820 items in it.
Return to Topics page
©Roger M. Palay
Saline, MI 48176 January, 2016
 That makes the confidence interval be
That makes the confidence interval be
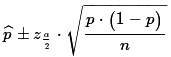
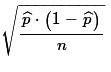 as
the approximation of the standard deviation of the
as
the approximation of the standard deviation of the
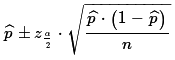




 and then realized that we had to use the approximation
involving
and then realized that we had to use the approximation
involving