or
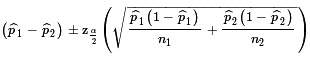
 and
and
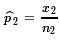 .
Then
.
Then 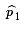 is an estimate of
p1,
is an estimate of
p1,
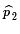 is an estimate of
p2, and
is an estimate of
p2, and
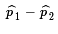 is an estimate of
p1 - p2.
is an estimate of
p1 - p2.
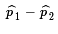 .
Then we need to know the distribution of the point estimate.
Under certain conditions we can consider
.
Then we need to know the distribution of the point estimate.
Under certain conditions we can consider
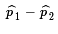 to be normal with mean
p1 - p2
and standard deviation, called the standard error,
to be normal with mean
p1 - p2
and standard deviation, called the standard error,
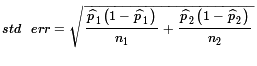 .
The required conditions are
.
The required conditions are
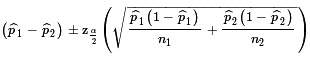
 = 43/66 ≈ 0.6515
= 43/66 ≈ 0.6515 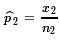 = 68/87 ≈ 0.7816
= 68/87 ≈ 0.7816 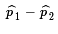 ≈ 0.6515 - 0.7816 = -0.1301
≈ 0.6515 - 0.7816 = -0.1301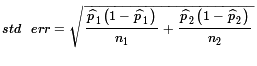 ≈
≈ 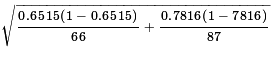 ≈ 0.735
≈ 0.735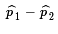 ± moe ≈ -0.1301 ± -0.144 ≈
(-0.2741, 0.0139)
± moe ≈ -0.1301 ± -0.144 ≈
(-0.2741, 0.0139)
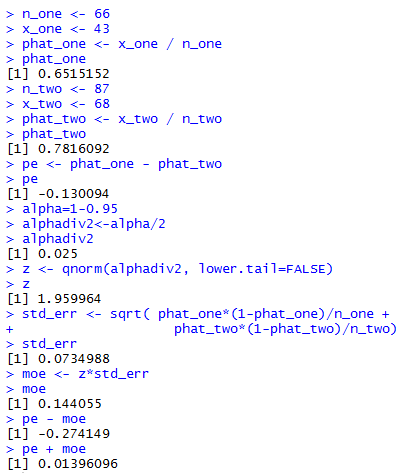
n_one <- 66
x_one <- 43
phat_one <- x_one / n_one
phat_one
n_two <- 87
x_two <- 68
phat_two <- x_two / n_two
phat_two
pe <- phat_one - phat_two
pe
alpha=1-0.95
alphadiv2<-alpha/2
alphadiv2
z <- qnorm(alphadiv2, lower.tail=FALSE)
z
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
std_err
moe <- z*std_err
moe
pe - moe
pe + moe
Figure 1 gives the console view of these commands.
# second example
n_one <- 74
x_one <- 24
phat_one <- x_one / n_one
phat_one
n_two <- 89
x_two <- 32
phat_two <- x_two / n_two
phat_two
pe <- phat_one - phat_two
pe
alpha=1-0.90
alphadiv2<-alpha/2
alphadiv2
z <- qnorm(alphadiv2, lower.tail=FALSE)
z
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
std_err
moe <- z*std_err
moe
pe - moe
pe + moe
The console view of those commands is shown in Figure 2.

ci_2popproportion <- function(
n_one, x_one, n_two, x_two, cl=0.95)
{
phat_one <- x_one / n_one
phat_two <- x_two / n_two
pe <- phat_one - phat_two
alpha=1-cl
alphadiv2<-alpha/2
z <- qnorm(alphadiv2, lower.tail=FALSE)
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
moe <- z*std_err
ci_low <- pe - moe
ci_high <- pe + moe
result <- c( ci_low, ci_high, moe,
std_err, z, alphadiv2,
phat_one, phat_two)
names( result ) <-
c("ci low", "ci_high", "M of E",
"Std. Err", "z-value", "alpha/2",
"p hat 1", "p hat 2")
return( result )
}
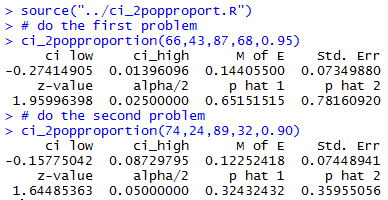
Once this function is defined, we can load it and use it
to solve the two problems presented above
via commands such as
source("../ci_2popproport.R")
# do the first problem
ci_2popproportion(66,43,87,68,0.95)
# do the second problem
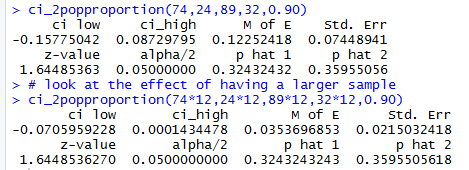
ci_2popproportion(74,24,89,32,0.90)
which produce the results shown in Figure 3.
ci_2popproportion(74*12,24*12,89*12,32*12,0.90)to generate a 90% confidence interval from samples that are 12 times the size of the Case 2 samples but that have exactly 12 times the number of successes in each sample. Thus, the sample proportions will not change even though the samples are much larger. To help look at the effect of having a larger sample Figure 4 first repeats the output of Case 2 and then shows the result of this new command.
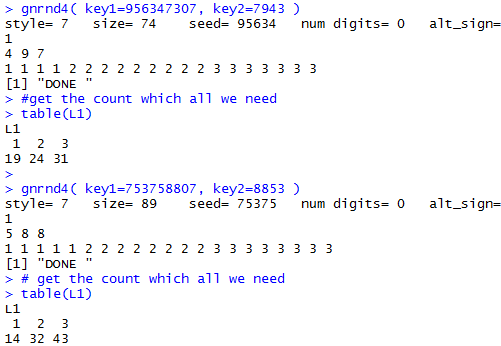
gnrnd4( key1=956347307, key2=7943 ) #get the count which all we need table(L1) gnrnd4( key1=753758807, key2=8853 ) # get the count which all we need table(L1)Which produce the console view shown in Figure 5.
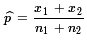 .
This is called the pooled sample proportion.
Using that pooled sample proportion gives us the standard error
defined by
.
This is called the pooled sample proportion.
Using that pooled sample proportion gives us the standard error
defined by 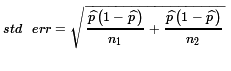 .
You may note that this is
algebraically equivalent to
.
You may note that this is
algebraically equivalent to
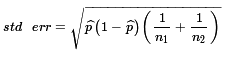 ,
a formula that is often used simply because it
is a slightly more efficient computation.
With all of this in hand we are ready to look at
using either the critical value or the
attained significance approach.
(It is worth noting that since this is a normal distribution,
and since the null hypothesis has the mean of the
difference of the proportions be 0, the two approaches
will be remarkably similar.)
,
a formula that is often used simply because it
is a slightly more efficient computation.
With all of this in hand we are ready to look at
using either the critical value or the
attained significance approach.
(It is worth noting that since this is a normal distribution,
and since the null hypothesis has the mean of the
difference of the proportions be 0, the two approaches
will be remarkably similar.)
 = 37/92 ≈0.402
and
= 37/92 ≈0.402
and
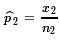 = 28/83 ≈0.337.
However, what we really want is the pooled sample proportion
= 28/83 ≈0.337.
However, what we really want is the pooled sample proportion
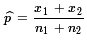 = (37+28)/(92+83) ≈0.3714.
These computations can be done in R via the commands
= (37+28)/(92+83) ≈0.3714.
These computations can be done in R via the commands
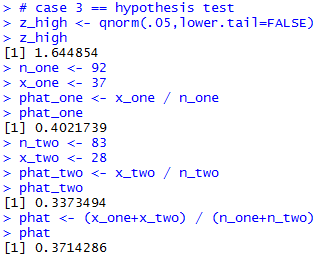
# case 3 == hypothesis test z_high <- qnorm(.05,lower.tail=FALSE) z_high n_one <- 92 x_one <- 37 phat_one <- x_one / n_one phat_one n_two <- 83 x_two <- 28 phat_two <- x_two / n_two phat_two phat <- (x_one+x_two) / (n_one+n_two) phatThe result of those commands is given in Figure 6.
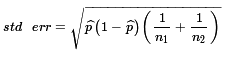 = 0.0731.
Then, the critical value will be the
product of our z value with 5% above it times this standard error,
or about 1.645*0.0731 ≈ 0.1203.
Therefore, we will reject H0 if the
difference in the sample proportions is greater than
the critical value 0.1203.
However, in this case the difference in the proportions is
about 0.0648, a value that is not greater than the
critical value and we say that we do not have sufficient evidence
to reject H0 at the 0.05 level of significance.
= 0.0731.
Then, the critical value will be the
product of our z value with 5% above it times this standard error,
or about 1.645*0.0731 ≈ 0.1203.
Therefore, we will reject H0 if the
difference in the sample proportions is greater than
the critical value 0.1203.
However, in this case the difference in the proportions is
about 0.0648, a value that is not greater than the
critical value and we say that we do not have sufficient evidence
to reject H0 at the 0.05 level of significance.
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) ) std_err crit_high <- z_high * std_err crit_high diff <- phat_one - phat_two diffFigure 7 holds the console image of those commands.

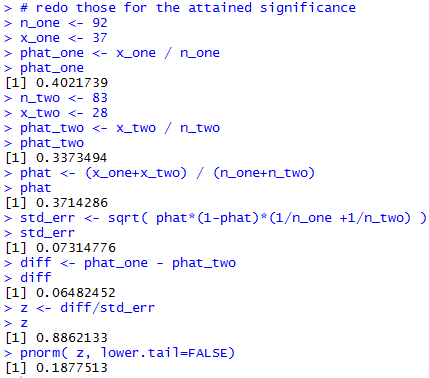
# redo those for the attained significance n_one <- 92 x_one <- 37 phat_one <- x_one / n_one phat_one n_two <- 83 x_two <- 28 phat_two <- x_two / n_two phat_two phat <- (x_one+x_two) / (n_one+n_two) phat std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) ) std_err diff <- phat_one - phat_two diff z <- diff/std_err z pnorm( z, lower.tail=FALSE)Figure 8 holds the console view of those statements.
 = 54/306 ≈0.1765
and
= 54/306 ≈0.1765
and
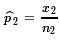 = 108/422 ≈0.2559.
However, what we really want is the pooled sample proportion
= 108/422 ≈0.2559.
However, what we really want is the pooled sample proportion
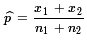 = (54+108)/(306+422) ≈0.2226.
These computations can be done in R via the commands
= (54+108)/(306+422) ≈0.2226.
These computations can be done in R via the commands
# case 4 == hypothesis test 2-sided z_high <- qnorm(.025,lower.tail=FALSE) z_high n_one <- 306 x_one <- 54 phat_one <- x_one / n_one phat_one n_two <- 422 x_two <- 108 phat_two <- x_two / n_two phat_two phat <- (x_one+x_two) / (n_one+n_two) phatThe result of those commands is given in Figure 9.
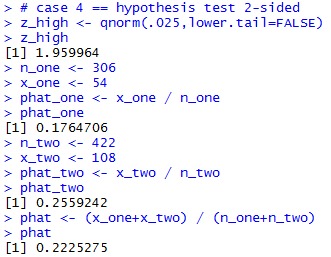
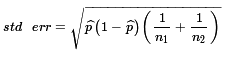 = 0.0312.
Then, the critical values will be the
product of our z values times this standard error,
or about -1.96*0.0312 ≈ -0.0612
and about 1.96*0.0312 ≈ 0.0612.
Therefore, we will reject H0 if the
difference in the sample proportions is
less than the critical value -0.0612 or
greater than
the critical value 0.0.0612.
In this case the difference in the proportions is
about -0.0794, a value that is less than the lower
critical value and we say that we
reject H0 at the 0.05 level of significance.
= 0.0312.
Then, the critical values will be the
product of our z values times this standard error,
or about -1.96*0.0312 ≈ -0.0612
and about 1.96*0.0312 ≈ 0.0612.
Therefore, we will reject H0 if the
difference in the sample proportions is
less than the critical value -0.0612 or
greater than
the critical value 0.0.0612.
In this case the difference in the proportions is
about -0.0794, a value that is less than the lower
critical value and we say that we
reject H0 at the 0.05 level of significance.
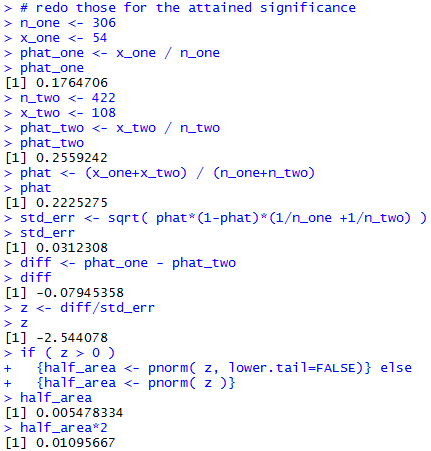
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) ) std_err crit_high <- z_high * std_err crit_high crit_low <- -z_high * std_err crit_low diff <- phat_one - phat_two diffFigure 10 holds the console image of those commands.

# redo those for the attained significance
n_one <- 306
x_one <- 54
phat_one <- x_one / n_one
phat_one
n_two <- 422
x_two <- 108
phat_two <- x_two / n_two
phat_two
phat <- (x_one+x_two) / (n_one+n_two)
phat
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
std_err
diff <- phat_one - phat_two
diff
z <- diff/std_err
z
if ( z > 0 )
{half_area <- pnorm( z, lower.tail=FALSE)} else
{half_area <- pnorm( z )}
half_area
half_area*2
Figure 11 holds the console view of those statements.
hypoth_2test_prop <- function(
x_one, n_one, x_two, n_two,
H1_type, sig_level=0.05)
{ # perform a hypothsis test for the difference of
# two proportions based on two samples.
# H0 is that the proportions are equal, i.e.,
# their difference is 0
# The alternative hypothesis is
# != if H1_type =0
# < if H1_type < 0
# > if H1_type > 0
# Do the test at sig_level significance.
phat_one <- x_one / n_one
phat_two <- x_two / n_two
phat <- (x_one+x_two) / (n_one+n_two)
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
diff <- phat_one - phat_two
if( H1_type==0)
{ z <- abs( qnorm(sig_level/2))}
else
{ z <- abs( qnorm(sig_level))}
to_be_extreme <- z*std_err
decision <- "Reject"
if( H1_type < 0 )
{ crit_low <- - to_be_extreme
crit_high = "n.a."
if( diff > crit_low)
{ decision <- "do not reject"}
attained <- pnorm( diff, mean=0, sd=std_err)
alt <- "p_1 < p_2"
}
else if ( H1_type == 0)
{ crit_low <- - to_be_extreme
crit_high <- to_be_extreme
if( (crit_low < diff) & (diff < crit_high) )
{ decision <- "do not reject"}
if( diff < 0 )
{ attained <- 2*pnorm(diff, mean=0, sd=std_err)}
else
{ attained <- 2*pnorm(diff, mean=0, sd=std_err,
lower.tail=FALSE)
}
alt <- "p_1 != p_2"
}
else
{ crit_low <- "n.a."
crit_high <- to_be_extreme
if( diff < crit_high)
{ decision <- "do not reject"}
attained <- pnorm(diff, mean=0, sd=std_err,
lower.tail=FALSE)
alt <- "p_1 > p_2"
}
result <- c( alt, n_one, x_one, phat_one,
n_two, x_two, phat_two,
phat, std_err, z,
crit_low, crit_high, diff,
attained, decision)
names(result) <- c("H1:",
"n_one","x_one", "phat_one",
"n_two","x_two", "phat_two",
"pooled", "Std Err", "z extreme",
"critical low", "critical high",
"difference",
"attained", "decision")
return( result )
}
Once this has been placed in the parent directory
under the name hypo_2popproport.R we can load and run
that function for the data in Case: 3 via the commands
source("../hypo_2popproport.R")
hypoth_2test_prop(37,92,28,83,1,0.05)
The console image of those two commands is shown in Figure 12.

hypoth_2test_prop(54,306,108,422,0,0.05)to produce the output shown n Figure 13.
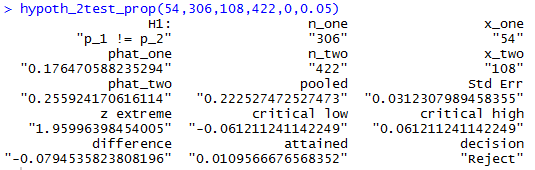
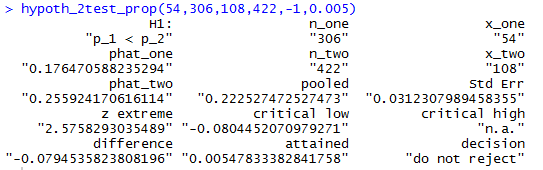
hypoth_2test_prop(54,306,108,422,-1,0.005)the result of which appears in Figure 14.
n_one <- 66
x_one <- 43
phat_one <- x_one / n_one
phat_one
n_two <- 87
x_two <- 68
phat_two <- x_two / n_two
phat_two
pe <- phat_one - phat_two
pe
alpha=1-0.95
alphadiv2<-alpha/2
alphadiv2
z <- qnorm(alphadiv2, lower.tail=FALSE)
z
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
std_err
moe <- z*std_err
moe
pe - moe
pe + moe
# second example
n_one <- 74
x_one <- 24
phat_one <- x_one / n_one
phat_one
n_two <- 89
x_two <- 32
phat_two <- x_two / n_two
phat_two
pe <- phat_one - phat_two
pe
alpha=1-0.90
alphadiv2<-alpha/2
alphadiv2
z <- qnorm(alphadiv2, lower.tail=FALSE)
z
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
std_err
moe <- z*std_err
moe
pe - moe
pe + moe
ci_2popproportion <- function(
n_one, x_one, n_two, x_two, cl=0.95)
{
phat_one <- x_one / n_one
phat_two <- x_two / n_two
pe <- phat_one - phat_two
alpha=1-cl
alphadiv2<-alpha/2
z <- qnorm(alphadiv2, lower.tail=FALSE)
std_err <- sqrt( phat_one*(1-phat_one)/n_one +
phat_two*(1-phat_two)/n_two)
moe <- z*std_err
ci_low <- pe - moe
ci_high <- pe + moe
result <- c( ci_low, ci_high, moe,
std_err, z, alphadiv2,
phat_one, phat_two)
names( result ) <-
c("ci low", "ci_high", "M of E",
"Std. Err", "z-value", "alpha/2",
"p hat 1", "p hat 2")
return( result )
}
source("../ci_2popproport.R")
# do the first problem
ci_2popproportion(66,43,87,68,0.95)
# do the second problem
ci_2popproportion(74,24,89,32,0.90)
# look at the effect of having a larger sample
ci_2popproportion(74*12,24*12,89*12,32*12,0.90)
gnrnd4( key1=956347307, key2=7943 )
#get the count which all we need
table(L1)
gnrnd4( key1=753758807, key2=8853 )
# get the count which all we need
table(L1)
# case 3 == hypothesis test
z_high <- qnorm(.05,lower.tail=FALSE)
z_high
n_one <- 92
x_one <- 37
phat_one <- x_one / n_one
phat_one
n_two <- 83
x_two <- 28
phat_two <- x_two / n_two
phat_two
phat <- (x_one+x_two) / (n_one+n_two)
phat
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
std_err
crit_high <- z_high * std_err
crit_high
diff <- phat_one - phat_two
diff
# redo those for the attained significance
n_one <- 92
x_one <- 37
phat_one <- x_one / n_one
phat_one
n_two <- 83
x_two <- 28
phat_two <- x_two / n_two
phat_two
phat <- (x_one+x_two) / (n_one+n_two)
phat
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
std_err
diff <- phat_one - phat_two
diff
z <- diff/std_err
z
pnorm( z, lower.tail=FALSE)
# case 4 == hypothesis test 2-sided
z_high <- qnorm(.025,lower.tail=FALSE)
z_high
n_one <- 306
x_one <- 54
phat_one <- x_one / n_one
phat_one
n_two <- 422
x_two <- 108
phat_two <- x_two / n_two
phat_two
phat <- (x_one+x_two) / (n_one+n_two)
phat
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
std_err
crit_high <- z_high * std_err
crit_high
crit_low <- -z_high * std_err
crit_low
diff <- phat_one - phat_two
diff
# redo those for the attained significance
n_one <- 306
x_one <- 54
phat_one <- x_one / n_one
phat_one
n_two <- 422
x_two <- 108
phat_two <- x_two / n_two
phat_two
phat <- (x_one+x_two) / (n_one+n_two)
phat
std_err <- sqrt( phat*(1-phat)*(1/n_one +1/n_two) )
std_err
diff <- phat_one - phat_two
diff
z <- diff/std_err
z
if ( z > 0 )
{half_area <- pnorm( z, lower.tail=FALSE)} else
{half_area <- pnorm( z )}
half_area
half_area*2
source("../hypo_2popproport.R")
hypoth_2test_prop(37,92,28,83,1,0.05)
hypoth_2test_prop(54,306,108,422,0,0.05)
hypoth_2test_prop(54,306,108,422,-1,0.005)