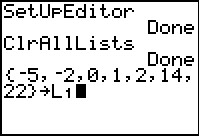
It is a good idea to set up the editor and to clear all prior
data from the lists on the calculator.
The sequence 

 will select, paste, and perform the SetUpEditor command. The sequence
will select, paste, and perform the SetUpEditor command. The sequence


 will select, paste, and
perform the ClrAllLists command.
will select, paste, and
perform the ClrAllLists command.
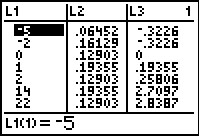
To store the list of data values from the table above in
L1 we enter the values, enclosed in curly-braces and separated by commas
and then store that into the desired list. The key seequences is
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
The display should appear as in Figure 1.
.
The display should appear as in Figure 1.

 to have the calculator perform it.
The calculator not only stores the values, it also displays the list on our screen,
this time without the commas.
to have the calculator perform it.
The calculator not only stores the values, it also displays the list on our screen,
this time without the commas.
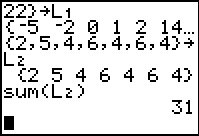
Our next task is to enter the probabilities into L2.
Again we will enter these directly. However, since all of the values have a denominator of 31
we will just enter the numerator at this time. Therefore, the lsit that we want to assign
to L2 is {2,5,4,6,4,6,4}.
We press the keys to generate that list and then use the
 key to assign it to L2.
The calculator redisplays the values.
key to assign it to L2.
The calculator redisplays the values.

We move to the LIST menu via
![]()
![]() .
Then we move to the MATH sub-menu.
The command that we want is the fifth one, sum(.
We press
.
Then we move to the MATH sub-menu.
The command that we want is the fifth one, sum(.
We press ![]() to select that command and paste it onto the main screen.
to select that command and paste it onto the main screen.


 and have it performed via
and have it performed via  .
We are happy to see that the sum is indeed 31.
.
We are happy to see that the sum is indeed 31.
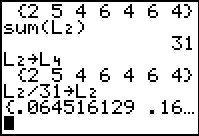
Then we can take care of dividing each value in
L2 by 31
by using ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
The calculator again displays the result, but given the values involved the
individual numbers use so many digits that we really only see one probability value
at a time. We could ask the calculator to display the values
in fractional form.
.
The calculator again displays the result, but given the values involved the
individual numbers use so many digits that we really only see one probability value
at a time. We could ask the calculator to display the values
in fractional form.
 .
We want the
.
We want the  .
.
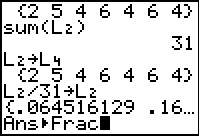
 to perform the task.
to perform the task.
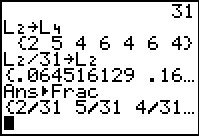
Another way to look at the values is to use the StatEditor.


 .
Here we see both the data values of L1
and the probability values, to 5 decimal places, in
L2.
.
Here we see both the data values of L1
and the probability values, to 5 decimal places, in
L2.








 , accomplishes
the first part of this, multiplying the specific values and putting the separate products
into corresponding elements of L3.
, accomplishes
the first part of this, multiplying the specific values and putting the separate products
into corresponding elements of L3.

 to paste that command to the main screen.
to paste that command to the main screen.
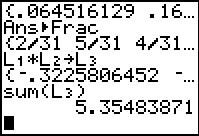


 .
The calculator does the task and gives the answer as 5.35483871.
.
The calculator does the task and gives the answer as 5.35483871.


 .
The calculator supplies the Ans seen on the screen.
Press
.
The calculator supplies the Ans seen on the screen.
Press  to perform the command.
to perform the command.
To get the variance of the data we want to
start by finding the squared differences
between the data values and the mean. The command
(L1–X)2 will do this.
We create that command and store the resutls in L5
via 







 .
Then press
.
Then press  to perform the command.
The calculator displays the
results after it stores them in L5.
to perform the command.
The calculator displays the
results after it stores them in L5.
Then we want to multiply those values by the probability values stored
in L2.
The key sequence

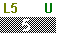






 creates and performs the command, putting the results in
L6.
creates and performs the command, putting the results in
L6.


 ,
move to the MATH sub-menu via
,
move to the MATH sub-menu via 
 , and then select the fifth option, sum(
via
, and then select the fifth option, sum(
via 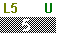 , and finish
the command with
, and finish
the command with 

 and then
with
and then
with  .
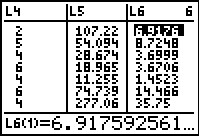
With that we find that the variance is 74.6805411.
.
With that we find that the variance is 74.6805411.
To get the standard deviation we just need to take the square root of the
variance. Press 
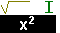 and then, to recall the answer we just calculated,
and then, to recall the answer we just calculated,

 and finish with
and finish with

 .
From this we see that the standard deviation is 8.641790388.
.
From this we see that the standard deviation is 8.641790388.

In Figure 11 we have moved to the STAT menu and then the CALC sub-menu
via 
 .
We select and paste the 1-Var Stats command by
pressing
.
We select and paste the 1-Var Stats command by
pressing  .
.
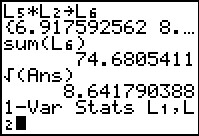
 to have the calcualtor perform the command.
to have the calcualtor perform the command.

There are two features of this display that need to be addressed. The first is that the indicated value of n is 1. The computation of the value of n is to add all of the values in the second list in the command, in this case, add all of the values in L2. Of course, those are all probabilities and we know that the sum of the probabilities asssigned to all the distinct values has to be 1. The second feature is that there is no value given for Sx. This will happen when the two lists that we give to the 1-Var Stats command represent discete values and their associated probabilities. (Actually, it seems that the calculator refrains from giving the values of Sx if the value of n is not a whole number greater than 1. This makes some sense because that is a clear indication that the values of the frequencies are not really frequencies.)

 to see the rest of the output from the
1-Var Stats stats command.
to see the rest of the output from the
1-Var Stats stats command.